3-17 837. 新 21 点
Date:2022-03-17 09:16:28
标签:
- 动态规划
题目:837. 新 21 点 ( 中等😕 )
该题难度较大,边界条件提交难想
爱丽丝参与一个大致基于纸牌游戏 “21 点” 规则的游戏,描述如下:
爱丽丝以 0 分开始,并在她的得分少于 k 分时抽取数字。 抽取时,她从 [1, maxPts] 的范围中随机获得一个整数作为分数进行累计,其中 maxPts 是一个整数。 每次抽取都是独立的,其结果具有相同的概率。
当爱丽丝获得 k 分 或更多分 时,她就停止抽取数字。
爱丽丝的分数不超过 n 的概率是多少?
与实际答案误差不超过 10-5 的答案将被视为正确答案。
示例
示例 1:
输入:n = 10, k = 1, maxPts = 10
输出:1.00000
解释:爱丽丝得到一张牌,然后停止。
示例 2:
输入:n = 6, k = 1, maxPts = 10
输出:0.60000
解释:爱丽丝得到一张牌,然后停止。 在 10 种可能性中的 6 种情况下,她的得分不超过 6 分。
示例 3:
输入:n = 21, k = 17, maxPts = 10
输出:0.73278
分析
动态规划
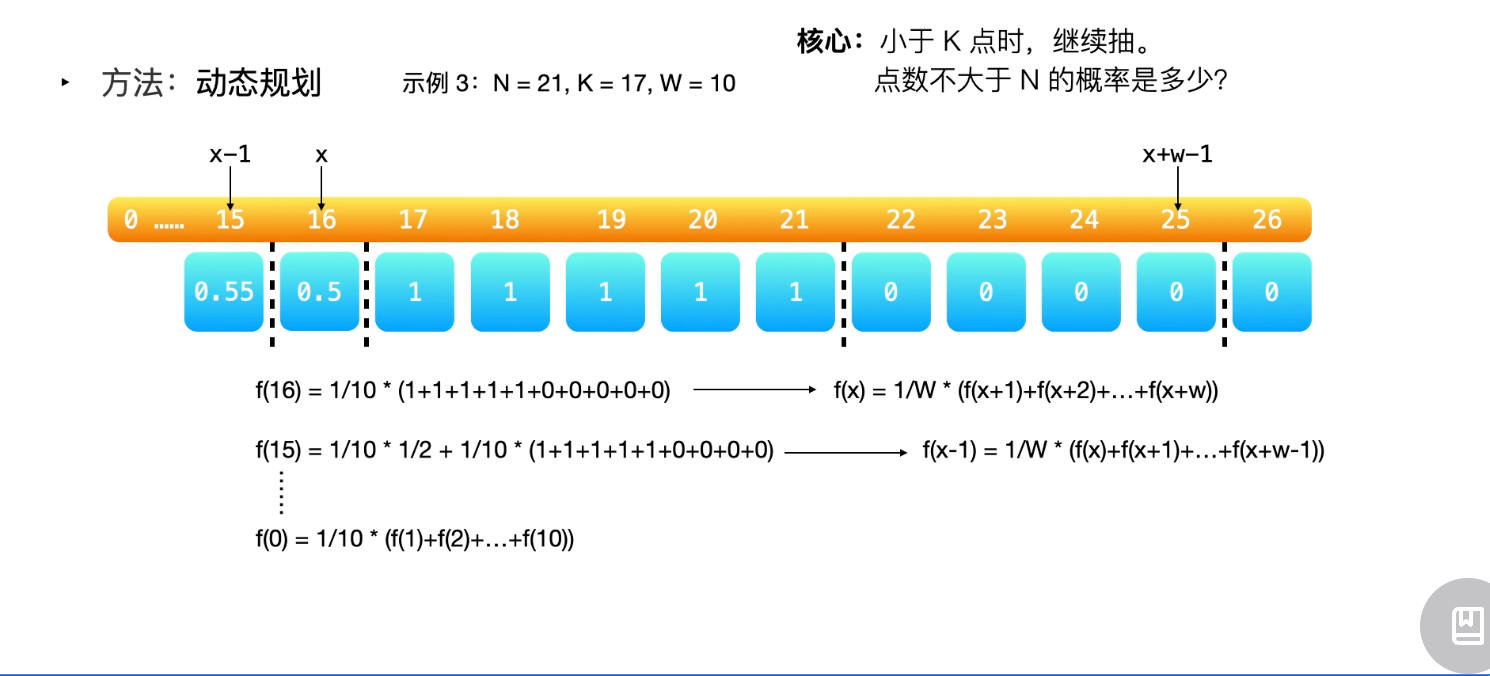
问题一:为什么 dp[0] 就是解?
dp[x]表示的是以 x 得分开始游戏时获胜的概率
这里,假设 N=21,K=17,W=10,那么 dp[16] 表示爱丽丝已经获得了 16 分,那么从 16 分开始游戏,她获胜的概率。同理,dp[0] 就表示爱丽丝已经获取了 0 分,从 0 分开始游戏,她获胜的概率是多少。根据递推公式,要求 dp[0]就先要求 dp[1],dp[2],...,dp[x+w-1],反向求解即可。
题解

优化求累加和
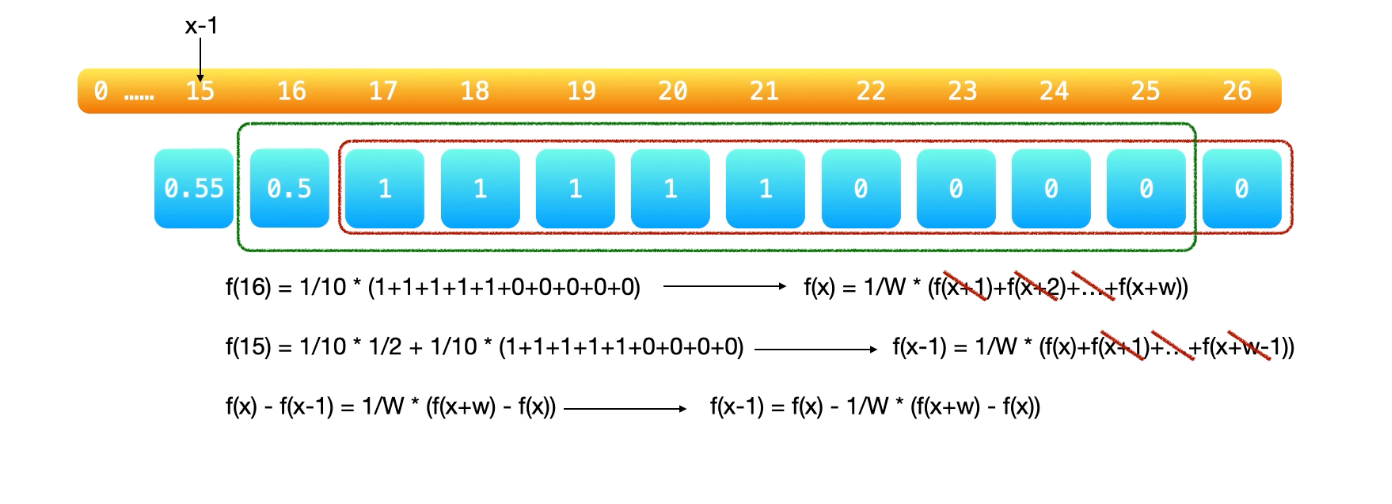

解决角标越界问题

function new21Game(n: number, k: number, maxPts: number): number {
const dp = new Array(k + maxPts).fill(0)
const minLen = Math.min(n + 1, k + maxPts)
for (let i = k; i < minLen; ++i) {
dp[i] = 1
}
let s = Math.min(n - k + 1, maxPts)
for (let i = k - 1; i >= 0; --i) {
dp[i] = s / maxPts
s += dp[i] - dp[i + maxPts]
// for (let j = i + 1; j < i + 1 + maxPts; ++j) {
// s += dp[j]
// }
}
return dp[0]
}
使用
function main() {
// const n = 10,
// k = 1,
// maxPts = 10
const n = 2,
k = 2,
maxPts = 3
console.log('[]:', new21Game(n, k, maxPts))
}
main()
export {}