3-5 5.最长回文子串

Date：2022-03-06 20:01:10

标签：

• 动态规划

  边缘扩散

题目：5. 最长回文子串 ( 中等😕 )

给你一个字符串 s，找到 s 中最长的回文子串。

示例

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

分析

• 暴力法：枚举所有的子串，判断是否为回文串

  耗时：枚举需要 O(n^2)，判断需要 O(n)，所以时间复杂度为 O(n^3)

• 动态规划，边缘扩散

  • 详细见：最长回文子串

  • 动态转移方程：

    P(i,j)=P(i+1,j−1)∧(Si==Sj)

    即： 如果[i+1, j-1]为回文，且 nums[i] === nums[j]，则[i, j]区间为回文，它们是相等关系

  • 下面是 size(当前区间个数)和 i、j 变化的图

    会发现，越到后面，[i+1, j-1] 的回文性就已经确定了

    比如，size=5 时，此时，[i+1, j-1] 的区间就是 b 和 b 的区间，而 b 和 b 的回文性在 size=3 的时候就求出来了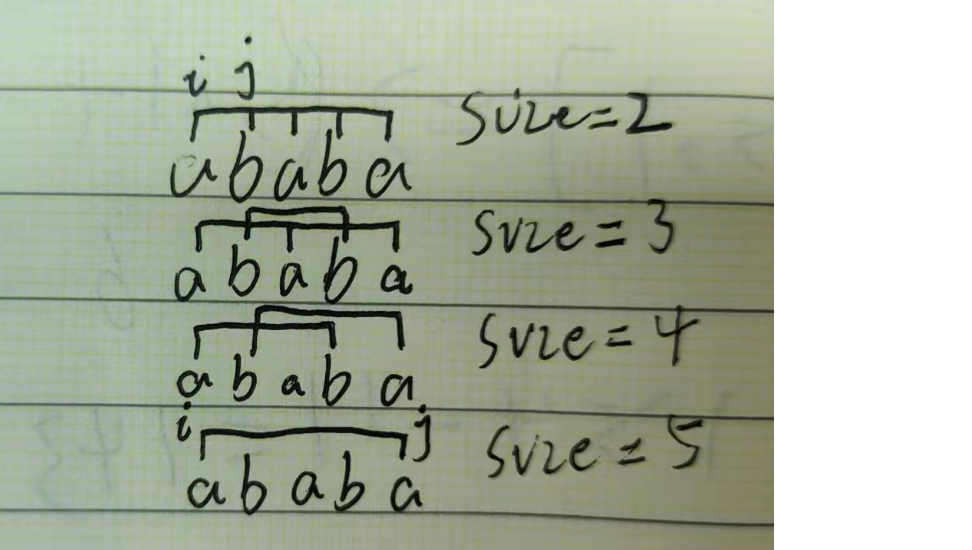

    

题解

动态规划

function longestPalindrome(s: string): string {
  const len = s.length
  // error:
  // const dep: boolean[][] = new Array(len).fill([])
  const dep: boolean[][] = new Array(len)
  let begin = 0,
    maxLen = 1

  // the substring's length is 1, so it is a palindrome
  for (let i = 0; i < len; ++i) {
    const newArr = new Array(len)
    newArr[i] = true
    dep[i] = newArr
  }

  for (let size = 2; size <= len; ++size) {
    for (let i = 0; i < len; ++i) {
      // size is [i, j]'s length
      // size = j - i + 1 ==> j = size + i -1
      const j = size + i - 1

      if (j >= len) {
        break
      }

      if (s[i] !== s[j]) {
        dep[i][j] = false
      } else {
        if (j - i + 1 <= 3) {
          dep[i][j] = true
        } else {
          dep[i][j] = dep[i + 1][j - 1]
        }
      }

      const newMaxLen = j - i + 1
      if (dep[i][j] && newMaxLen > maxLen) {
        maxLen = newMaxLen
        begin = i
      }
    }
  }

  return s.substring(begin, begin + maxLen)
}

使用

function main() {
  // const s = 'babbd'
  const s = 'cbbd'

  console.log('[]:', longestPalindrome(s))
}

main()

export {}

扩展 0：根据下标计算数组的长度

const len = j - i + 1

const j = len + i - 1
const i = j - len + 1

扩展 1：Js 中初始化二维数组？

我想初始化一个 3x3 的存放 boolean 值的二维数组，怎么操作呢？

可能会这样写：

const len = 3

const dp: boolean[][] = new Array(len).fill(new Array(len).fill(true))

// =>> 输出
// [
//   [true, true, true],
//   [true, true, true],
//   [true, true, true],
// ]

看起来，符合预期，我尝试修改第 0 行第 1 个元素为 false

dp[0][1] = false
console.log('[dp]:', dp)

// =>> 输出
// [
//   [true, false, true],
//   [true, false, true],
//   [true, false, true],
// ]

嗯？为什么第 2 行，第 3 行也变了

猜测，Array.fill 填充的是同一个数组对象，即三个数组引用地址是一样的

正确写法

const len = 3
const dp: boolean[][] = new Array(len)

for (let i = 0; i < len; ++i) {
  dp[i] = new Array(len).fill(true)
}

输出

;[
  [true, true, true],
  [true, true, true],
  [true, true, true],
]